Analisis Klasifikasi Penyakit Hewan dengan K-Nearest Neighbors (K-NN)

Analisis klasifikasi penyakit hewan menggunakan algoritma K-Nearest Neighbors (K-NN). Artikel ini mencakup dataset, konversi data kategorikal ke numerik, normalisasi data, perhitungan jarak Euclidean, dan prediksi menggunakan K-NN.

  Artificial Intelligence   Febuari 28, 2025   0   62  Tambahkan ke Daftar Bacaan
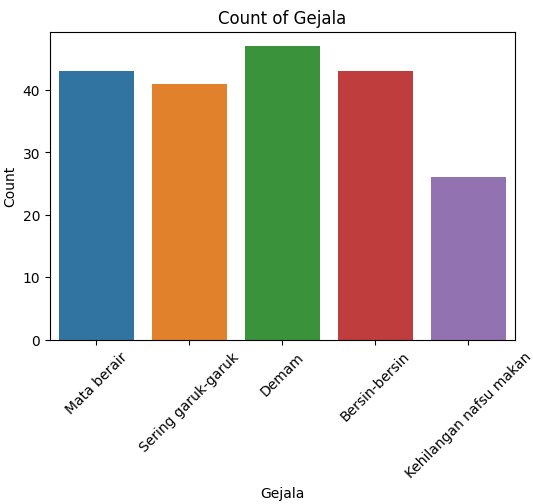
Analisis Klasifikasi Penyakit Hewan dengan K-Nearest Neighbors (K-NN)

1. Dataset yang Digunakan

Dataset yang digunakan terdiri dari fitur-fitur sebagai berikut:

  • Umur Hewan (dalam tahun)
  • Jenis Kelamin (Jantan/Betina)
  • Lingkungan (Indoor/Outdoor)
  • Pola Makan (Seimbang/Tidak Seimbang)
  • Kontak Hewan Sakit (Ada/Tidak Ada)
  • Gejala
  • Durasi Gejala (dalam hari)
  • Tingkat Keparahan (skala 1-5)
  • Jenis Penyakit (Menular/Tidak Menular)

Dataset Mentah:

Umur Hewan Jenis Kelamin Lingkungan Pola Makan Kontak Hewan Sakit Gejala Durasi Gejala Tingkat Keparahan Jenis Penyakit
3 tahun Jantan Indoor Tidak Seimbang Ada Mata besar 7 hari 4 Menular
2 tahun Jantan Outdoor Tidak Seimbang Ada Sering garuk-garuk 10 hari 4 Menular
5 tahun Betina Indoor Seimbang Tidak Ada Demam 3 hari 1 Tidak Menular
1 tahun Jantan Indoor Tidak Seimbang Tidak Ada Bersin-bersin 5 hari 4 Menular
2 tahun Betina Outdoor Seimbang Tidak Ada Kehilangan nafsu makan 5 hari 3 Tidak Menular

2. Konversi Data Kategorikal ke Numerik

  • Jenis Kelamin: Jantan = 1, Betina = 0
  • Lingkungan: Indoor = 0, Outdoor = 1
  • Pola Makan: Seimbang = 0, Tidak Seimbang = 1
  • Kontak Hewan Sakit: Ada = 0, Tidak Ada = 1
  • Jenis Penyakit (Target): Menular = 0, Tidak Menular = 1

3. Normalisasi Data

Normalisasi dilakukan dengan rumus:

X′=X−XminXmax−XminX' = \frac{X - X_{min}}{X_{max} - X_{min}}

Normalisasi untuk setiap fitur:

  • Umur Hewan

    • Xmin=1X_{min} = 1, Xmax=5X_{max} = 5
    • Contoh: Untuk umur 3 tahun: X′=3−15−1=0.5X' = \frac{3 - 1}{5 - 1} = 0.5

  • Durasi Gejala

    • Xmin=3X_{min} = 3, Xmax=10X_{max} = 10
    • Contoh: Untuk durasi 7 hari: X′=7−310−3=0.57X' = \frac{7 - 3}{10 - 3} = 0.57

Lakukan normalisasi ini untuk semua fitur dalam dataset.

4. Perhitungan Jarak Euclidean

Misalkan kita ingin mengklasifikasikan seekor kucing baru dengan fitur berikut:

Umur Hewan Jenis Kelamin Lingkungan Pola Makan Kontak Hewan Sakit Gejala (encoded) Durasi Gejala Tingkat Keparahan
4 1 0 1 1 2 5 2

Menghitung jarak ke setiap data dalam dataset dengan rumus:

D(A,B)=(x2−x1)2+(y2−y1)2+...+(z2−z1)2D(A,B) = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + ... + (z_2 - z_1)^2}

Contoh perhitungan jarak ke data pertama:

D=(0.75−0.5)2+(1−1)2+(0−0)2+(1−1)2+(1−0)2+(2−3)2+(5−7)2+(2−4)2D = \sqrt{(0.75 - 0.5)^2 + (1 - 1)^2 + (0 - 0)^2 + (1 - 1)^2 + (1 - 0)^2 + (2 - 3)^2 + (5 - 7)^2 + (2 - 4)^2} D=(0.25)2+0+0+0+1+1+4+4D = \sqrt{(0.25)^2 + 0 + 0 + 0 + 1 + 1 + 4 + 4} D=10.25≈3.2D = \sqrt{10.25} \approx 3.2

Perhitungan dilakukan untuk setiap titik dalam dataset.

5. Menentukan K dan Prediksi

Jika kita memilih K=3K = 3, maka kita mengambil 3 tetangga terdekat berdasarkan jarak Euclidean. Jika mayoritas dari tetangga terdekat memiliki label "Menular", maka prediksi untuk kucing baru juga "Menular".

Dari hasil perhitungan jarak, jika lebih banyak tetangga terdekat memiliki penyakit Menular, maka kucing baru diprediksi juga memiliki penyakit Menular.

Metode K-NN ini membantu dalam mengklasifikasikan penyakit hewan berdasarkan pola gejala dan karakteristik lainnya. Model ini dapat dikembangkan lebih lanjut dengan penyesuaian nilai K, teknik penyaringan fitur, atau penggunaan model pembelajaran mesin lainnya untuk meningkatkan akurasi prediksi.

Tags

Apa Reaksi Anda?

like

dislike

love

funny

angry

sad

wow